Центр 
искомой окружности принадлежит серединному перпендикуляру к отрезку 
Обозначим 
середину отрезка 
— основание перпендикуляра, опущенного из точки на прямую 
— точку пересечения серединного перпендикуляра с прямой 
(см. рисунок а). Из условия касания окружности и прямой следует, что отрезки 
и 
равны радиусу 
окружности. Заметим, что точка не может лежать по ту же сторону от прямой 
что и точка 
так как в этом случае расстояние от точки до прямой меньше, чем расстояние от нее до точки 
Из прямоугольного треугольника 
с катетом 
и 
находим, что 
Так как 
и 
получаем: 
и, следовательно, 
Из прямоугольного треугольника 
в котором 
находим:
В результате получаем уравнение для : Возведем в квадрат обе части этого уравнения и приведем подобные члены. Получим уравнение 
решая которое находим два корня 
Если радиус равен 
то центром окружности является точка
(см. рисунок б). 
Ответ: 
или 
Другое решение
Пусть точка касания окружности с прямой лежит на луче (см. рисунок a). По теореме о касательной и секущей
откуда 
Пусть — точка пересечения луча 
и перпендикуляра к проведенного через точку 
Из прямоугольного треугольника 
находим: Таким образом, точка удалена от точек 
и на одно и то же расстояние, равное 
Следовательно, — центр искомой окружности, а ее
радиус равен Пусть теперь точка 
касания окружности с прямой лежит на продолжении за точку 
(см. рисунок б), а прямая, проходящая через точку перпендикулярно пересекает прямую 
в точке 
а окружность вторично — в точке 
Тогда Если — радиус окружности, то 
По теореме о двух секущих
то есть 
откуда находим, что 
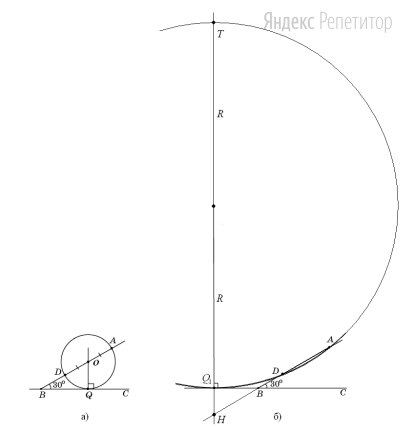
Ответ: или Возможны другие формы записи ответа. Например,
-
- радиус окружности равен
или
равного 
взята такая точка 
что
и 
